Chinlone Game
I developed it with XNA Framework for Microsoft Imagine Cup 2013. Although it was selected for the first round of compeition (around 50 groups), it did not pass the second round. I particulry chose Chinlone Game because it is quite unique in that it is Non Zero-Sum Game, in which no one is losing. At that time, I was studying Game Theory, and found that Chinlone as a Non-Zero Sum Game is interesting.
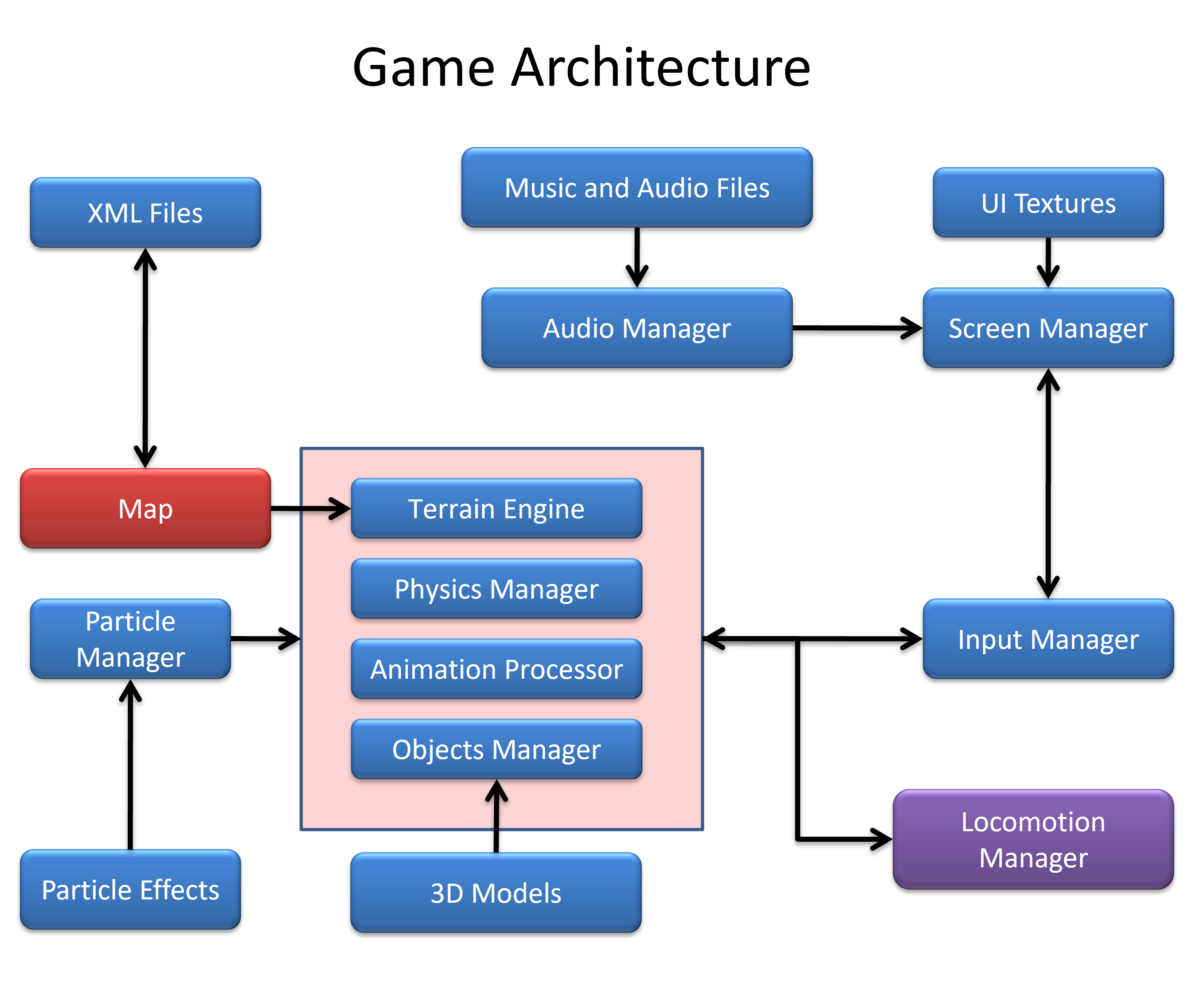
The basic game architecture invovles various components for basic game engine: physics engine (RK4 Integration), terrain generator, locomotion manager, and so on.
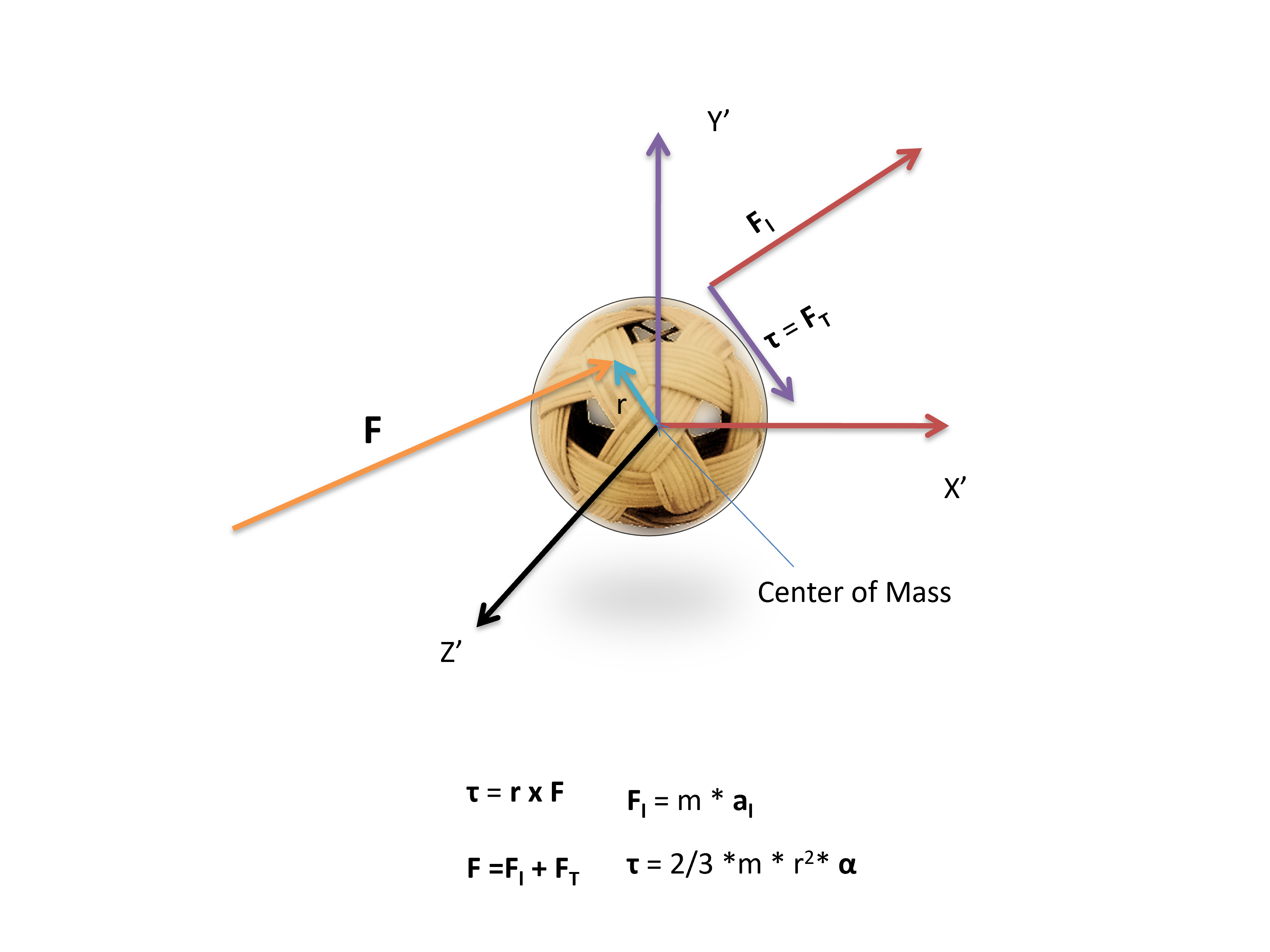
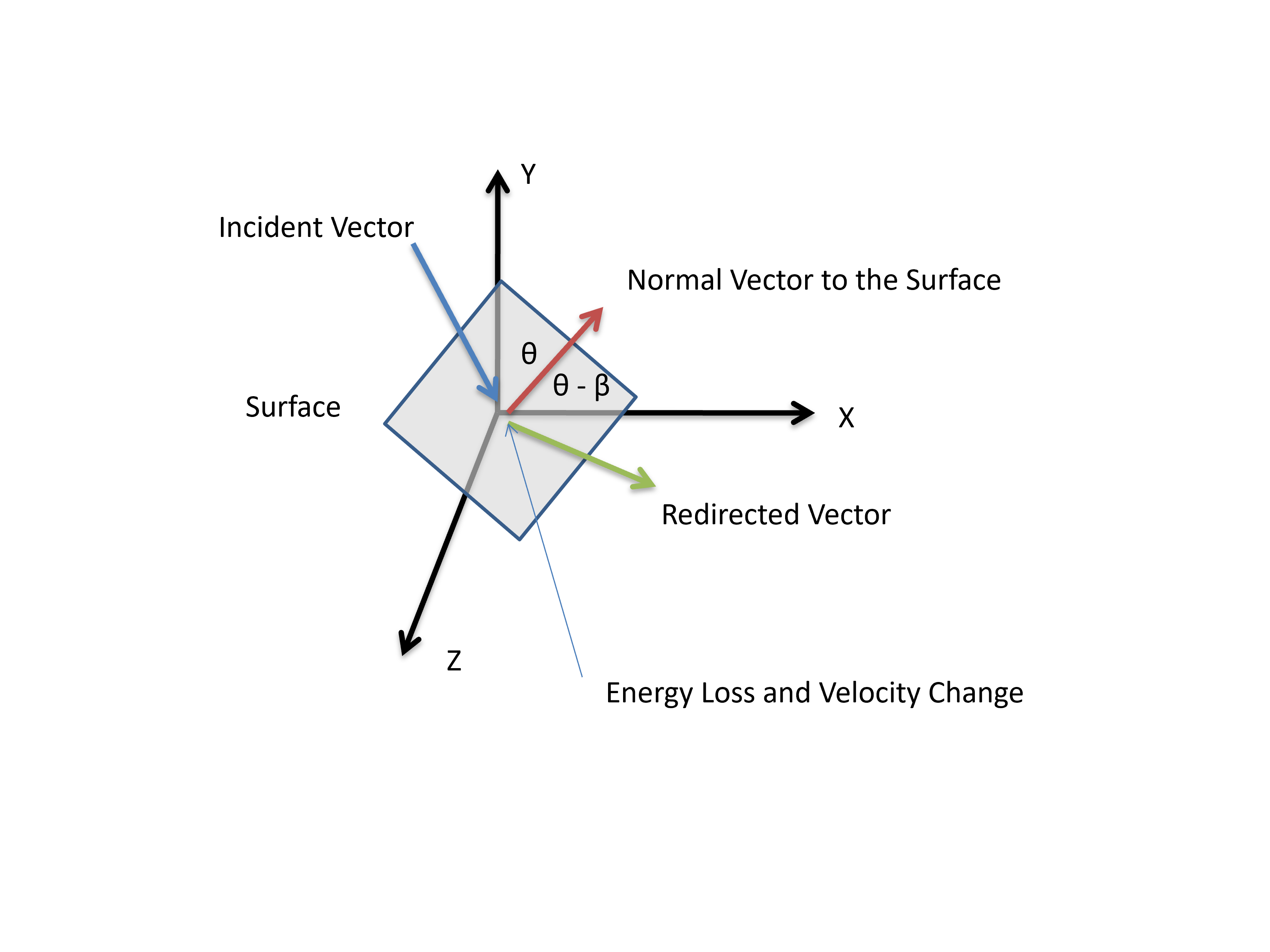
I used RK4 Integration method to calculate all the physics, except for animation, which uses "Forward Kinematics". There are two scenarios: hit by the game character and bounce on the ground.
using System; using System.Collections.Generic; using System.Linq; using System.Text; using Microsoft.Xna.Framework; using Microsoft.Xna.Framework.Graphics; using Microsoft.Xna.Framework.Input; namespace GameEngine { ////// There will two major forces acting on the physical objects. /// The first one is the Gravity. W = m * g; /// The second one is the Thrust exerted by Character. F = m * a; /// When there is no collision between Character and Physical Objects, there will be only one force, Gravity. /// Also, Gravity will be acting on all objects all the time. /// public static class PhysicsManager { #region "Constants" public const float MinimumKE = 0.0001f; public static Vector3 Gravity = new Vector3(0, -0.003f, 0); public static Vector3 Thrust = new Vector3(0.0f, 0.06f, 0.0f); public static float DampingRatio = 0.02f; public static float ForcePower = 0.03f; public static float TimeStamp = 100.0f; #endregion #region "Methods" public static Derivitive Differentiate(State s, float t, Vector3 F, Vector3 T) { Derivitive output = new Derivitive(); output.Velocity = s.Velocity; output.Spin = s.Spin; Forces(s, t, out output.Force, out output.Torque, F, T); return output; } public static Derivitive Differentiate(State s, float t, float dt, Derivitive ds , Vector3 F, Vector3 T) { s.Position += ds.Velocity * dt; s.Momemtum += ds.Force * dt; s.Orientation += ds.Spin * dt; s.AngularMomemtum += ds.Torque * dt; s.ReCalculate(); Derivitive output = new Derivitive(); output.Velocity = s.Velocity; output.Spin = s.Spin; Forces(s, t + dt, out output.Force, out output.Torque,F, T); return output; } public static State Integrate(State s, float t, float dt, Vector3 F, Vector3 T) { Derivitive a = Differentiate(s, t,F,T); Derivitive b = Differentiate(s, t, 0.5f * dt, a,F, T); Derivitive c = Differentiate(s, t, 0.5f * dt, b,F, T); Derivitive d = Differentiate(s, t, dt, c,F,T); s.Position += 1.0f/6.0f * dt * (a.Velocity + 2.0f * (b.Velocity + c.Velocity) + d.Velocity); s.Momemtum += 1.0f/6.0f * dt * (a.Force + 2.0f * (b.Force + c.Force ) + d.Force); s.Orientation += Quaternion.Multiply((a.Spin + Quaternion.Multiply((b.Spin + c.Spin),2.0f) + d.Spin),1.0f / 6.0f * dt); s.AngularMomemtum += 1.0f / 6.0f * dt * (a.Torque + 2.0f * (b.Torque + c.Torque) + d.Torque); return s; } public static void Forces(State s, float t, out Vector3 F1, out Vector3 T1, Vector3 F2, Vector3 T2) { F1 = Gravity + F2; T1 = DampingRatio * T2; } //Cuboid Inertial Tensor public static Matrix CuboidTensor(float mass, float l, float w, float h) { float x = mass * (l*l + h*h) / 12.0f; float y = mass * (l*l + w*w) / 12.0f; float z = mass * (w*w + h*h) / 12.0f; Matrix m = new Matrix ( x, 0, 0, 0, 0, y, 0, 0, 0, 0, z, 0, 0, 0, 0, 0 ); return m; } //Hollow Sphereical Inertial Tensor public static Matrix SphericalTensor(float mass, float r) { float x = 2.0f / 3.0f * mass * r * r; Matrix m = new Matrix ( x, 0, 0, 0, 0, x, 0, 0, 0, 0, x, 0, 0, 0, 0, 0 ); return m; } #endregion } }